Четыре заключенных в шляпах. Интересная логическая задача про тюрьму

Четыре заключенных в шляпах. Интересная логическая задача про тюрьму

В тюрьме становится довольно тесно, и тюремщик думает об освобождении некоторых из заключенных. Однако они должны решить интересную логическую задачу. Если они потерпят неудачу, то они возвращаются в свои камеры, и другая группа заключенных получит шанс выйти. Этот интересный процесс выглядит следующим образом. Десять заключенных будут отобраны, и им будет поставлена задача. Они имеют право разговаривать на данном этапе, и планировать свою стратегию. Потом они должны включить свою логику…

Заключенные будут выстроены в одну шеренгу, все смотрят в одном направлении. Заключенный сзади, может увидеть все девять заключенных перед ним. Заключенный впереди не видит никаких других заключенных, так как они все за ним. Заключенные, стоящие в остальной части линии, будут иметь возможность видеть заключенных перед ними, но не тех, что за ними.
После того, заключенные стоят в очереди, каждый заключенный получает шляпу на голову. Шляпа будет черной или белой. Выбор цвета в каждом случае совершенно случайный. Ни один заключенный не может видеть цвета своей шляпы. Заключенный может видеть цвет шляпы заключенных, которые стоят перед ним, но не может видеть цвет шляпы, которые одеты на  заключенных стоящих за его спиной.
Каждый заключенный, должен угадать цвет шляпы, которая на нем и сказать его вслух. Они могут говорить только одно слово - "белый" или "черный". Первый должен догадаться заключенный, стоящий на задней линии. Затем заключенный перед ним, и так далее. Последний будет говорить заключенный, стоящий на передней линии.
Тюремщик знает, что это серьезная логическая задача. Он позволит допустить не более одной ошибки, таким образом, остальные девять догадок должны быть верны. В таком случае, все десять заключенных будут освобождены. Интересно, что если случится более одной ошибки, все заключенные будут возвращены в свои камеры.
Что является лучшей стратегией, которую заключенные могут принять? Каковы их шансы получить свободу?
Ответ на этот вопрос на следующей странице …
Здесь нет никаких уловок. Только логика и математика.

Задача эйлера о шляпах. Здравый смысл и задача о разноцветных шляпах

Моя(уже, как и я сам, бородатая)задачка-головоломка про 100 мудрецов, выстроенных в ряд с надетыми на них разноцветными шляпами, как недавно выяснилось, получила неожиданное продолжение, ставящее этот сюжет в один ряд с парадоксом Банаха-Тарского…
Вот вольный перевод на русский язык этого продолжения.
Рассмотрим такую вариацию этой задачи: cчётное множество мудрецов выстроены в натуральный ряд (лицом в сторону возрастания ряда, так что каждый видит перед собой бесконечное число мудрецов). Можно считать, что каждый из мудрецов знает свой номер в последовательности. Каждому мудрецу надета на голову шляпа одного из допустимых цветов, и каждому задается вопрос о цвете его шляпы. Всех, кто дает неправильный ответ, казнят. В отличие от конечного варианта , мудрецы не слышат чужих ответов на заданные им вопросы (и не видят казней неправильно ответивших коллег) и, следовательно, не могут получать никакой новой информации. Тем не менее, они могут заранее договориться так, чтобы казнено было лишь конечное число мудрецов.
Решение этой задачи выглядит вроде бы так.
Назовем две разных цветовых последовательности принадлежащими к одному классу , если они совпадают, начиная с некоторого момента. По аксиоме выбора, из каждого класса можно выбрать по одному различному "представителю" - то есть сопоставить каждому классу одну конкретную последовательность цветов, причем все эти последовательности будут различными. Заставим мудрецов запомнить это сопоставление. Тогда, видя перед собой бесконечное число шляп, каждый мудрец легко определяет класс , в который входит данная последовательность, и отвечает на заданный ему вопрос, называя тот цвет, который находится на данном месте в последовательности-"представителе". Поскольку все последовательности одного класса различаются только в каком-то (заведомо конечном) количестве начальных позиций, то казнено могут быть только конечное число мудрецов.
В "ручной" версии я специально ограничил кол-во последовательностей счетным множеством, чтобы использовать не чистую аксиому выбора, а прямую конструкцию для установления соответствия. Однако аксиома выбора не требует счетности числа множеств - следовательно, "абстрактная" версия решения работает и в более общем случае.
Это решение кажется парадоксальным и удивительным, потому что даже для двух цветов вероятность одному отдельно взятому мудрецу угадать свой цвет равна 1/2, а значит, ожидаемая доля казненных не должна быть менее 1/2 и уж точно не должна стремиться к 0. Но совсем уж фантастичным этот результат выглядит для счётного числа цветов , а ведь приведенное доказательство обобщается и на этот случай - то есть несмотря на то, что вероятность спасти одного человека равна 0 , в целом по-прежнему удается спастись всем, кроме конечного числа людей!!

Загадка про 4 заключенных ответ. Тюремные загадки: большой сборник тюремных загадок и ответов

Еще один пример нестандартного поста, которым любит баловать своих читателей OFFICEPLANKTON.

Сборник очень необычных для законопослушного гражданина загадок с подвохом. В определенных местах исходя из вашего ответа, может случится дальнейшая ваша судьба.

С подобными тюремными головоломками часто сталкивались известные люди, работавшие в СИЗО в период молодости. Обычно тюремные задачки задают новичкам в камере ради забавы, но сама тюремная задачка и ответ на нее, скажет многое сокамерникам о новичке.

В дальнейшем сокамерники относятся к человеку, исходя из того, как тот ответил на каверзные вопросы.

Просьба впечатлительным лицам, лицам младше 18 лет, и лицам с неустойчивой психикой не читать данный материал. Содержит ненормативную лексику.

Зеки сами по себе народ очень изобретательный. И даже если на воле арестант был компьютерщиком, то в местах лишения свободы у него могут открыться скрытые таланты в изобретательстве.

Так например зеки умело умеют приспосабливаться к тяжелой жизни благодаря смекалке, и тюремным изобретениям из подручных материалов.

С помощью изобретений, арестанты могут вскипятить воду, или подкурить сигарету.

1Два стула (классика):

Есть два стула, на одном пики точены, на другом х*и др*чены, на какой сядешь, на какой мать посадишь?
Ответ: Возьму пики точены, срублю х*и др*чены, сам сяду и мать посажу.
Ответ №2: Сам на пики сяду, мать на колени посажу.

2 Парашют:

Ты летишь на парашюте, справа — лес ху*в, слева — море гов*а. Куда будешь садиться?
Ответ: В каждом лесу есть поляна, а в каждом море — островок.

3Яма:

Ты упал в яму. В яме пирожок и х*й. Что съешь, что в *опу засунешь?
Ответ: Возьму пирожок и вылезу из ямы.

4*опа или мать?

В Ж*пу дашь или мать продашь?
Ответ: Ж*па не дается, мать не продаётся.

5Вилка:

Вопрос в лоб: Вилкой в глаз или в ж*пу раз?
Ответ: А на зоне вилок нету.
Ответ №2: Что-то я здесь одноглазых не вижу.

6Мыло или хлеб?

Что съешь — мыло со стола или хлеб с параши?
Ответ: Стол не мыльница, параша не хлебница.

7Про Сахару:

Ты с кентом идешь по пустыне Сахаре. На расстоянии ста километров нет ни жилья, ни населенных пунктов, никого и ничего, кроме песка.

Вдруг выползает ядовитая змея, бросается на кента и кусает его за х*й. Что делать будешь?
Ответ: Если у кента залупа выше колена, то змея не достанет. Если ниже — то он сам отсосет.

Ответ №2: Сегодня кент, а завтра мент.

8Про поезд:

Ты едешь в поезде, прикованный к рычагам, ими можно повернуть или влево, или вправо. Впереди развилка — справа мать к столбу привязана, слева кенты, человек десять. Куда свернешь, кого задавишь?
Ответ: Сегодня кенты, а завтра менты.
Ответ на все загадки, приведенные выше: Проснусь.

9Про кости:

Сидит зек на шконаре, открывают кормушку и дают баланду, хлеб сухой. Утром опять открывают кормушку и видят кости. Вопрос: откуда кости, если зек живой?
Ответ: Кости игральные.

10Про петухов:

Жили были два петуха, одного е*ли до обеда, а другого после обеда, кому было хуже?
Ответ: У кого уже тому и хуже.

11Футбол:

Рисуют на стене футбольные ворота, а на полу мяч. Говорят забить гол. Что будешь делать?
Ответ: Попроси дать пас.

12Веник:

Тебе дают в руги веник и говорят: «Сыграй на гитаре что-нибудь». Что будешь делать?
Ответ: Отдай веник со словами «А ты настрой сначала»

13Зашей бутылку:

Бутылку разбивают и говорят: «Зашей». Что будешь делать?
Ответ: Попроси вывернуть наизнанку.

14Баян:

Просят сыграть на батарее, как на баяне. Что будешь делать?
Ответ: Попроси раздуть меха.
А если вам интересно, как проходит жизнь в тюрьме — можем предложить довольно необычные и интересные рассказы о жизни в тюрьме.

15Посадили мужика в тюрьму на 9 лет:

Посадили мужчину в тюрьму на строгих 9 лет.

Однажды ему кум (начальник тюрьмы) говорит, отгадаешь загадку в течении 9 лет отпущу тебя, ну мужик согласился и начальник говорит: Слово из 9 букв, есть в каждом доме, кончается на «зор», но не ТЕЛЕВИЗОР.

Мужик думал думал долгих 9 лет так и не отгадал. Отсидел он свои 9 лет приходит домой заходит в дом и видит этот предмет и умирает от сердечного приступа.

Ответ: Телевизор. Вопрос не про то, что загадал тюремщик, а про предмет, про кот.мужик сначала услышал от тюремщика(телевизор), а затем увидел дома. И если вчитаться в условие, то можно это понять.

Загадка про заключенных и шляпы ответ. Три мудреца и парадокс

Есть загадка про трех мудрецов, которые спорили о том, кто из них самый мудрый.
Проходивший мимо путешественник решил им помочь в споре. Он достал пять шляп . Три черные и две белые.
Сказал, что наденет каждому мудрецу на голову по шляпе, так что тот будет видеть шляпу других, но не свою. Кто первый определит какого цвета шляпа на нем (черная или белая) тот, мол, самый мудрый.
Но путешественник схитрил и надел на всех черные шляпы. Через некоторое время один из мудрецов сказал, что на нем шляпа черная. Вопрос как он это определил?
Ответ и парадокс подкатом:
Ответ:
Первый мудрец рассуждал от обратного. «Если на мне белая шляпа, то второй мудрец, не зная какая шляпа на нем, сделает два предположения. 1-ое если шляпа на нем белая. То третий бы сразу сказал, что на нем черная шляпа. Раз он этого не говорит значит(должен был сделать вывод второй мудрец) 2 -ое, шляпа на нем черная. Но раз и второй мудрец молчит(рассуждал мудрец первый) значит на мне не может быть белой шляпы и она черная.
Парадокс:
В жизни все могло произойти по-другому сценарию. Допустим, что путешественник не схитрил и дал шапки в разнобой. Самый мудрый из них, просчитался бы в том моменте, что остальные два его собеседника идиоты. Создав длинную цепочку из рассуждений он (сидя в белой шапке(!!!)) сделал бы громогласное заявление о том, что он в шапке черной.(на основе того лишь, что два его собеседника дауна, не могут создать хоть сколько нибудь длинную логическую последовательность) Естественно самого умного, те два дурака осмеют и он будет с позором исключен из общества мудрецов, как невежда.

Источник: https://interesnyefakty.com/stati/chetyre-zaklyuchennyh-prigovoreny-k-kazni-ochen-interesnaya-logicheskaya-zagadka-pro

Задача про четырех преступников. 6 логических задачек, которые встряхнут ваш ум

Эти задачи можно решить с ходу, жуя бутерброд в обеденный перерыв. А можно сломать весь мозг, но так и не сообразить, где тут правда и в чем подвох.

1. Загадка о заключенных

4 заключенных приговорены к казни.

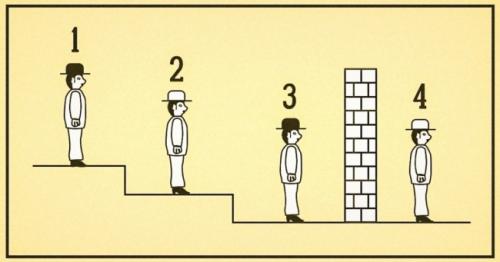
На них надели две белые шляпы и две черные шляпы. Мужчины не знают, какого цвета шляпы они носят. Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:

Заключенный № 1 может видеть заключенных № 2 и № 3.

Заключенный № 2 может видеть заключенного № 3.

Заключенный № 3 не видит никого.

Заключенный № 4 не видит никого.

Судья любому заключенному, назвавшему цвет своей шляпы, пообещал свободу.

Вопрос: Кто назвал цвет своей шляпы первым?

Ответ.

4-й и 3-й заключенные молчат, потому что вообще ничего не видят.

1-й заключенный молчит, потому что видит перед собой шляпы разного цвета: у 2-го и 3-го. Соответственно у него либо белая, либо черная шляпа.

2-й заключенный, понимая, что 1-й молчит, делает вывод о том, что у него шляпа не такого цвета, как у 3-го, а именно белого цвета.

Вывод: Первым назвал цвет своей шляпы заключенный № 2.

2. Трудности на дороге

Один человек, меняя колесо у своей машины, уронил все 4 гайки крепления в решетку канализационного стока. Достать их оттуда невозможно. Водитель уже решил, что застрял на дороге надолго, но тут проходящий мимо ребенок посоветовал, как закрепить колесо. Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.

Вопрос: Что посоветовал ребенок?

Ответ.

Отвернуть по 1 гайке от оставшихся 3 колес и закрепить ими 4-е.

3. Явка провалена

Человеку нужно было проникнуть в секретный клуб, не вызвав подозрений. Он заметил, что все приходящие сначала отвечали на вопросы охранника и лишь затем входили. Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.

Вопрос: Почему?

Ответ.

На первый взгляд кажется, что пароль — это результат деления названного числа на 2. На самом деле это количество букв в предложенных числах. Верный ответ не 21, а 8.

4. Подарок Бабы-яги

Лето уже закончилось, когда Иван-царевич, направлявшийся в тридевятое царство за невестой, попросил ночлега в избушке на курьих ножках. Баба-яга ласково встретила гостя, напоила, накормила, спать уложила. На следующее утро она проводила Ивана-царевича с таким напутствием: «Встретится тебе по дороге река, моста через нее нет — придется тебе плыть. Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.

Вопрос: Почему?

Ответ.

Иван-царевич был у Бабы-яги в сентябре. Отсчитываем 100 дней и узнаем, что зима уже в разгаре. Река скована льдом, и ее можно спокойно перейти и без кафтана.

5. Клетки с кроликами

Во дворе стояли в ряд 3 большие клетки, окрашенные в разные цвета: красный, желтый и зеленый. В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.

Вопрос: Какого цвета была левая клетка?

Ответ.

Клетка была желтая. Задача подсказывает, что в зеленой клетке кроликов было вдвое больше — следовательно, их там четное количество. После того как из левой клетки забрали пятерых, в ней осталось тоже четное количество (так как легко разделилось пополам). Значит, до взятия количество кроликов было нечетным. Таким образом, левая клетка — не зеленая. Но и не красная, что видно из условия задачи.

6. Кто виноват?

Поздно вечером в одном из переулков неизвестная машина сбила человека и скрылась. Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения:

• «Машина синего цвета, за рулем был мужчина».
• «Машина шла на большой скорости и с погашенными фарами».
• «Машина была с номерным знаком и шла не очень быстро».
• «Машина „Москвич“ шла с погашенным светом».
• «Машина без номерного знака, за рулем была женщина».
• «Машина „Победа“, серого цвета».

Когда задержали автомобиль, выяснилось, что лишь один свидетель сообщил верные сведения. Остальные пятеро — по одному правильному и одному неправильному факту.

Назовите марку, цвет и скорость автомобиля. Имела ли машина номерной знак, шла ли она со светом и кто ее вел: мужчина или женщина?

Ответ.

Это была «Победа», синего цвета, с номерным знаком. Шла на большой скорости и с погашенными фарами. За рулем была женщина. Ориентируемся на показания постового — высокая скорость автомобиля. Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.

7. Бонус

Так что же делают одновременно все люди на Земле?

Ответ.

Становятся старше.

Загадка про цвет шляпы ответ.

4 человека стоят в ряд. Каждый может видеть только стоящих перед ним, если ничего не мешает. Первый видит второго и третьего. Второй видит третьего. Третий никого не видит из-за стены. Четвертый тоже никого не видит. Они знают, что на них одеты шляпы, две черные и две белые. Но никто из них не знает шляпа какого цвета одета на нем самом. Перед ними поставлена задача узнать про цвет своей шляпы. На свою шляпу смотреть нельзя, назад смотреть тоже нельзя. Вопрос: Кто из них в данной ситуации может узнать цвет своей шляпы?

3

Решение

4 шляпы 2-х цветов, первый видит 2 шляпы и у него 2 варианта: чёрный и белый. Второй понимает, что раз первый не может определить, значит шляпы у него и у 3-го человека разного цвета. Стало быть раз перед ним стоит человек в белой шляпе, значит сам он в чёрной.

ответил 2013-07-22T19:53:31.000000+04:00 6 лет, 7 месяцев назад

Ruffianshings

395

Еще 2 ответа

Итак… Первый может видеть или две шляпы одинакового цвета или разного.

1. Первый видит две шляпы одинакового цвета. Тогда он может сказать, какая шляпа на нем (если видит две белые, то на нем черная и наоборот). Как только первый сказал какая на нем шляпа, все остальные тоже могут сказать. Если первый сказал "На мне белая" (и, следовательно, на втором и третьем черная), то второй и третий могут сказать "на мне черная" и четвертый может сказать "на мне белая" . И наоборот: если первый сказал "На мне черная", то второй и третий скажут "на мне белая", а четвертый скажет "на мне черная". Причем четвертый может не ждать, пока скажут второй и третий. Как только четвертый услышит, что сказал первый, он может смело говорить, что на нем шляпа такого же цвета, как на первом.
2. Первый видит две шляпы разных цветов. Тогда он молчит (так как на нем может быть и белая, и черная). Если первый молчит, значит, второй понимает, что на нем и на третьем шляпы разных цветов! Тогда он, смотря на третьего, может назвать цвет своей шляпы (если на третьем - белая, на втором черная и наоборот). Как только третий услышал, что сказал второй, он говорит, что на нем шляпа другого цвета, чем на втором. В этом случае первый и четвертый не смогут сказать, какая на них шляпа, так как возможны два варианта.

Вот так!

ответил 2013-09-11T17:44:51.000000+04:00 6 лет, 5 месяцев назад

Emptiverefor

46

Первый видит второго и третьего. Соответственно он видит что на втором белая шляпа а на третьем чёрная (логически он может догадаться что на нём чёрная) то есть цвета шляп меняются через одного и логически он может догадаться.

Источник: https://interesnyefakty.com/stati/kto-nazval-cvet-svoey-shlyapy-pervym-zagadka-o-zaklyuchennyh