Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса
Теорема Фалеса интересные факты. Интересные факты из жизни Фалеса

Интересные факты из жизни Фалеса. По легенде теорема была сформулирована в не сохранившейся «Морской астрономии» Фалеса или Фоки Самосского. Ни одно из античных свидетельств, касающихся Фалеса, с этой теоремой никак напрямую не связано. Возможно, что теорема приписана Фалесу опосредованно, поскольку известно, что он умел измерять высоту обелиска и расстояние до корабля в море; при этих измерениях можно использовать подобие треугольников, а утверждение о пропорциональности сторон подобных треугольников доказывается на основе «теоремы Фалеса». Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга. Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла. Основы геометрии Фалес постигал в Египте.
Слайд 4 из презентации «Математические открытия» к урокам математики на тему «История математики»Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке математики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Математические открытия.pptx» можно в zip-архиве размером 622 КБ.
История математики
краткое содержание других презентаций об истории математики
«Математические открытия» - О теореме Пифагора. Теорема Пифагора. Великие открытия Архимеда. Открытия Архимеда. Фалес Милетский. Пифагорейцы. Творцы математики и их открытия. Сочинения Пифагора. Интересные факты из жизни Фалеса. Эратосфен Киренский. Труды Эратосфена. Мудрец. Решето Эратосфена. Теорема Фалеса. Начала Евклида. Описание монохорда.
«Математика в Греции» - Греческая математика поражает прежде всего красотой и богатством содержания. Успехи пифагорейцев в стереометрии были значительными. Математика в Древней Греции. Теэтет и Евклид установили классификацию квадратичных иррациональностей. Глава II. 1.2 Поворотный пункт в истории античной математики. Пифагорейцы заложили основы геометрической алгебры.
«Математика в США» - Джон фон Нейман. Чёрч стал профессором математики в Принстоне в 1929 году. Такой ответ поставил часового в тупик. Владимир Александрович Воеводский — российский и американский математик, преподаватель. Обозначение нуля также применялось для обозначения бесконечности. Американские премии в области математики.
«История математики в России» - Способ умножения с «помощью рук». Сухарева башня. Курбатов. Согласно показанию Курбатова, желающих учиться в школе было много. Материальная сторона дела была передана в Оружейную палату. Труд Магницкого. Первая математическая школа в Москве. Образование. А. Курбатов предложил Петру I математика. Арифметика.
«История появления математики» - Кипу, использовались инками для записи чисел. Рене Декарт. Листья на ветке растения. Математика в разное время. М.В.Остроградский. Интересные факты. Цифры майя. Математика. Математический закон Бенфорда. Великие математики. Исаак Ньютон. Разделы математики. История математики. Как появилась математика.
Источник: https://interesnyefakty.com/stati/fales-miletskiy-interesnye-fakty-geometriya-kratkaya-biografiya
Теорема Фалеса ударение. Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A A 1 | | B B 1 | | C C 1 | | D D 1 {\displaystyle AA_{1}||BB_{1}||CC_{1}||DD_{1}} и при этом A B = C D {\displaystyle AB=CD} .
- Проведём через точки A {\displaystyle A} и C {\displaystyle C} прямые, параллельные другой стороне угла. A B 2 B 1 A 1 {\displaystyle AB_{2}B_{1}A_{1}} и C D 2 D 1 C 1 {\displaystyle CD_{2}D_{1}C_{1}} . Согласно свойству параллелограмма: A B 2 = A 1 B 1 {\displaystyle AB_{2}=A_{1}B_{1}} и C D 2 = C 1 D 1 {\displaystyle CD_{2}=C_{1}D_{1}} .
Как разделить отрезок на 3 равные части по теореме Фалеса. Теорема Фалеса и деление отрезка в заданном отношении

Давно о геометрии не говорили, а о теореме ФАлеса (или ФалЕса?) вообще мало говорят. Хотя она весьма полезна. Начнем с формулировки, которая весьма не вразумительна, чем и объясняется не популярность данной теоремы.
Мутно, долго, не понятно. Мне больше нравится другая формулировка.
Тоже не понятно, но элегантно и коротко.
Задачи, которые решаются с помощью данной теоремы, довольно специфичны. Но есть одна задача на построение, которую можно встретить в реальной жизни. Это задача о делении отрезка в заданном отношении.
Суть вопроса: Дан отрезок. Его нужно поделить на два куска, чтобы их длины относились, как 2 : 5. Кусков может быть сколько угодно и отношение, может быть каким угодно. Алгебраически задача решается крайне легко: находим общее количество частей (2 + 5 = 7), делим длину отрезка на общее количество частей, находим длину каждого куска.
Но алгебраическое решение не всегда прокатывает. Например, мы не можем найти длину отрезка, или при делении получаются не целые числа. Тогда можно воспользоваться геометрическим способом.
Во-первых, проводим луч из конца отрезка. Любой, в любую сторону.
Дальше, на этом луче от точки А откладываем 7 (общее количество частей) равных отрезков.
Последнюю получившуюся точку - J соединяем с точкой В, а затем через каждую точку луча проводим прямую параллельную JB.
Таким образом, мы разделили отрезок АВ на 7 равных частей (по теореме Фалеса). Отсчитываем две части и ставим точку. Получаем: AK : KB = 2 : 5.
Вот таким простым образом, вы можете поделить свою комнату с соседом в любом отношении. Если вам кажется, что построение такого количества параллельных прямых дело сложное, то подумайте о перпендикулярах.
Докажите теорему Фалеса. Обобщенная теорема Фалеса
Определение, которое мы сформулировали, является избыточным – чтобы треугольники были подобны, не нужно требовать и пропорциональности трех пар сторон, и равенства трех углов.
Для того чтобы убедиться в том, что два треугольника являются подобными, существуют признаки подобия треугольников (по аналогии с признаками равенства). И в них не требуется проверять все утверждения, перечисленные в определении.
Чтобы разобраться в этом, рассмотрим очень древний и очень удобный геометрический инструмент – теорему Фалеса. Фалес Милетский, именем которого названа теорема, жил более 2,5 тысяч лет назад.

Рис. 8. Фалес Милетский
Теорема Фалеса достаточно наглядна и не вызывает особых сомнений даже без строгого доказательства: если параллельные прямые отсекают равные отрезки на одной стороне угла, то они отсекают равные отрезки и на другой стороне (см. рис. 9).
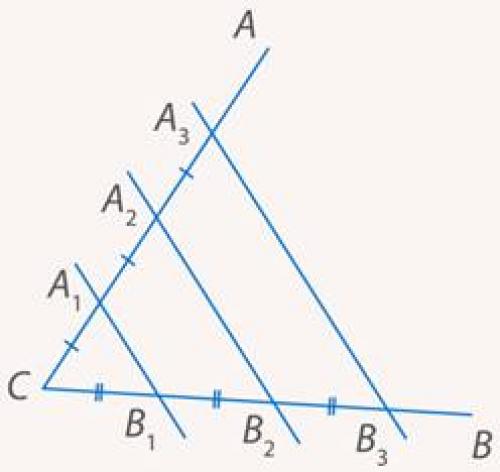
Рис. 9. Иллюстрация к теореме Фалеса
Более общая формулировка этой теоремы (ее еще называют обобщенной теоремой Фалеса или теоремой о пропорциональных отрезках ): параллельные прямые отсекают на сторонах угла пропорциональные отрезки .
Т. е. если пересечь угол несколькими параллельными прямыми (в отличие от классической формулировки можно начертить прямые на разных расстояниях друг от друга), то отношение двух отрезков на одной стороне угла будет равно отношению соответствующих отрезков на второй стороне (см. рис. 10):
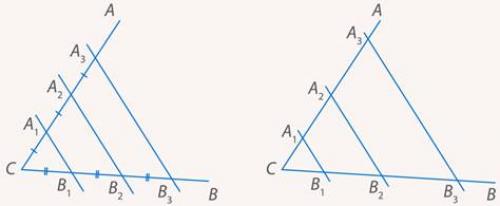
Рис. 10. Иллюстрация к теореме Фалеса
Доказывать эти теоремы мы пока не умеем. Но обязательно сделаем это чуть позже. Пока возьмем их на вооружение как известные нам факты.
Теорема Фалеса в жизни
Чтобы проиллюстрировать применение теоремы Фалеса, рассмотрим такой пример.
Пусть два корабля движутся так, что их курс друг относительно друга не меняется (под курсом в данном случае мы понимаем угол между направлением движения судна и направлением на второе судно) (см. рис. 11).
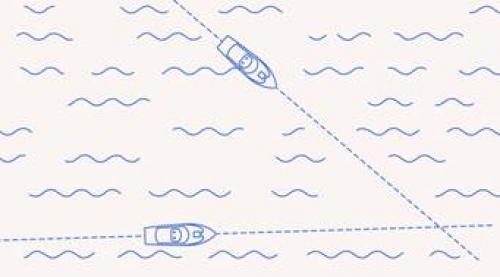
Рис. 11. Курс двух движущихся кораблей друг относительно друга не меняется
Тогда ясно, что при неизменности ситуации, неизбежно столкновение (поскольку из равенства углов следует, что прямые, соединяющие корабли, параллельны друг другу, а значит, за равные промежутки времени они проходят одинаковые расстояния и должны сойтись в одной точке – вершине угла) (см. рис. 12).
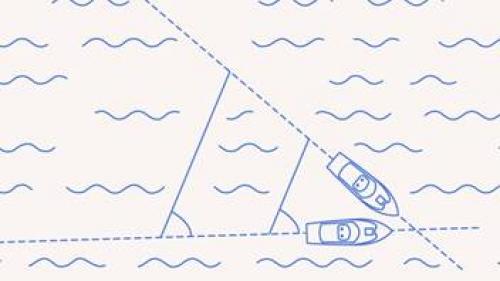
Рис. 12. За равные промежутки времени корабли проходят одинаковые расстояния и должны сойтись в одной точке
Это можно использовать для предотвращения аварий в море. Ведь чем раньше капитаны кораблей узнают о вероятности столкновения, тем больше шансов его избежать.
В отличие от автомобилей большие грузовые суда имеют очень большой тормозной путь (т. к. сила сопротивления со стороны воды очень маленькая, а инертность из-за большой массы огромная). Так, у нефтяных танкеров тормозной путь может быть длиной несколько десятков километров.