Масса или вес, как правильно. В чем разница массы и веса и почему возникает подмена понятий?

Масса или вес, как правильно. В чем разница массы и веса и почему возникает подмена понятий?

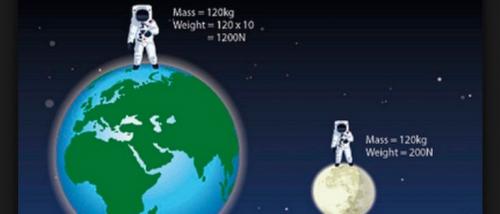
Сегодня мы с вами поднимем казалось бы незначительную, но на деле очень важную тему. А именно мы разберем, в чем разница массы и веса. Выпускник школы знает, что вес и масса – не одно и то же. Но даже самый титулованный физик не скажет продавцу: «Отмассте» мне килограмм яблок. Он произнесёт «взвесьте», имея в виду количество яблочного продукта, а не его тяжесть.  Раскроем загадку такого положения вещей.

Полистаем учебник физики

Вес – это сила, переменная величина, измеряется  ньютонами, означает воздействие на опору лежащего предмета или натяжение подвеса. Масса – это количество вещества внутри тела, исчисляется  килограммами, тоннами, фунтами и т.д., является постоянной величиной.

Для неподвижных объектов значения этих параметров прямо пропорциональны.  При взвешивании определяется усилие, с которым товар давит на подставку, а табло показывает его массу. Очень удобно продавцам и покупателям.

Когда возникает различие

Разница между двумя категориями физики становится видна, если меняется коэффициент пропорциональности. Назовём его К. В покое в условиях Земли он равен ускорению свободного падения  g=9,8. Примеры, когда вес меняется:

• Чем дальше от центра Земли, тем g меньше, а тело легче.
• Инерция. При взлёте самолёта или ракеты пилот испытывает перегрузки. Это к его тяжести добавилась инерция старта, и давление на опору (кресло) усилилось. Наоборот, при движении лифта вниз, пассажир становится легче, меньше давит на пол.
• Падающий предмет ничего не весит, так как  К= g — g=0. Это состояние невесомости, хотя  масса осталась той же.
• В условиях других планет сила тяжести меняется. На Луне g=1,62, а на Марсе 3,86. Одно и то же тело на Луне  легче в 6 раз, на Марсе – в 2,5 раза, чем в земных условиях.

Почему случается путаница

Человек воспринимает мир через ощущения. Мы не можем чувствовать массу, но способны ощутить вес. Девушка держит книгу. При этом ладонь – опора. Книга давит, рука сопротивляется. Читательница чувствует усилие по удержанию книжки. Противодействие — единственный способ определения массы, данный нам природой. Отсюда причина подмены  понятий, несоответствия норм языка физическим явлениям.

Надеюсь, что теперь вам понятно, в чем же эта разница. Ну а мы в свою очередь рекомендуем вам узнать, чем месса нетто отличается от брутто .

Вес или масса изделия. Масса или вес

Много лет назад, заканчивая школу, я был полностью уверен, что при взвешивании чего либо мы определяем вес тела, и уже зная его, можем вычислить его массу, разделив полученное значение на ускорение свободного падения. Мир, в который я пришел с этими знаниями был для меня незыблемым, так как мне казалось, что за школьные годы я овладел важным фундаментальным знанием и знал что такое вес, и что такое масса.
Некоторая неловкость была с единицами измерения. Вес измерялся в каких-то килограмм-силах, а масса в килограммах. Когда я приходил в магазин или на рынок, мне почему-то всё взвешивали в килограммах, а не в килограмм-силах. Было странно, но для повседневной жизни не критично.
Более серьезное неудобство возникло, когда пришлось пользоваться таблицами плотности вещества. Из курса физики я знал, что плотность измеряется отношением массы тела к объёму который оно занимает. Собственно это подтверждается и единицей измерения плотности, которая приводится в каждой таблице: кг/м куб. Казалось бы ситуация предельно проста. Измеряем объём тела, умножаем его на табличное значение плотности и получаем значение массы. Для того чтобы узнать сколько тело весит это значение необходимо умножить на ускорение свободного падения.
И вот тут возникла первая серьезная неприятность. Значения плотности в таблицах приведены не в массах, а в весе. Это уже был серьезный звоночек. Чтобы вычислить массу тела с использованием табличных данных, приходилось все время держать в уме, что это в расчете получается не масса, а вес, который уже отдельным действием надо приводить к массе.
Извращенность физики приучала к извращенному мышлению: читаем одно, думаем о другом, пишем третье.
Но даже к такой круговерти гибкое человеческое мышление адаптируется. Но вот то, что у нас международный эталон массы в один килограмм, оказался равным одной килограмм-силе, уже находится за гранью какого либо понимания.
Эталон массы выполнен из платины в виде цилиндра с одинаковой высотой и диаметром: 39 мм, т.е. имеет объём 46,59 см куб.
Один килограмм это 1000 грамм. Делим 1000 г на 46,59 см куб. Получаем 21,46 г/см куб.
Это значение соответствует плотности платины выраженной… в ВЕСЕ!
Вот с такой неразберихой наука претендует на исключительность знаний об окружающем нас мире.
Чему уж тут удивляться, что многие люди просто не видят разницы между весом и массой, если даже на международном уровне такая мешанина явление обычное.
Справедливости ради следует отметить, что неразбериха с массой и весом вызвана применяемыми в настоящее время единицами измерения.
В международной системе СИ вес как сила должен измеряться в Ньютонах, а в обыденной практике и технических расчетах применяют килограмм-силу (кгс), которая соответствует 9,8 Н и представляет собой силу которую развивает тело массой в 1 кг и ускорением свободного падения. Поэтому когда вес измеряется в кгс, то численно он равен массе тела в кг.
Поскольку переход от массы к весу должен иметь некую формульную зависимость, но которую в справочниках не приводят, то пользователь сам должен догадываться что в данном случае подразумевал составитель того или иного справочника.
Не удобно, но жить можно.

Что такое масса. Масса

I

Ма́сса (Massa)

Исаак (1587, Харлем, Нидерланды, — после мая 1635, там же или в Лиссе), голландский купец и резидент в России в 1614—34. Жил в Москве в 1601—09, 1612—34. Изучил русский язык и собрал много материалов по истории страны конца 16 — начала 17 веков и её географии. Около 1611 написал сочинение о событиях в России конца 16 — начала 17 веков — важный источник по истории крестьянской войны под предводительством И. И. Болотников а и других событий 1601—1609. Статьи М., посвященные истории и географии Сибири, были одним из первых сочинений о Сибири в западноевропейской литературе. М. опубликовал ряд карт России и отдельных её районов.

Соч.: Краткое известие о Московии в начале XVII в., М., 1937.

II

Ма́сса (от лат. massa — глыба, масса)

1) большое количество, крупное скопление чего-либо. 2) Полужидкое или тестообразное, бесформенное вещество; смесь (полуфабрикат) в различных производствах (например, бумажная масса). 3) См. Масса в физике.

III

Ма́сса

физическая величина, одна из основных характеристик материи, определяющая её инерционные и гравитационные свойства. Соответственно различают М. инертную и М. гравитационную (тяжёлую, тяготеющую).

Понятие М. было введено в механику И. Ньютон ом . В классической механике Ньютона М. входит в определение импульса (количества движения (См. Количество движения )) тела: импульс p пропорционален скорости движения тела v ,

p = mv . (1)

Коэффициент пропорциональности — постоянная для данного тела величина m — и есть М. тела. Эквивалентное определение М. получается из уравнения движения классической механики

f = ma . (2)

Здесь М. — коэффициент пропорциональности между действующей на тело силой f и вызываемым ею ускорением тела a . Определённая соотношениями (1) и (2) М. называется инерциальной массой, или инертной массой; она характеризует динамические свойства тела, является мерой инерции тела: при постоянной силе чем больше М. тела, тем меньшее ускорение оно приобретает, то есть тем медленнее меняется состояние его движения (тем больше его инерция).

Действуя на различные тела одной и той же силой и измеряя их ускорения, можно определить отношения М. этих тел: m₁ : m₂ : m₃ … = a₁ : a₂ : a₃ …; если одну из М. принять за единицу измерения, можно найти М. остальных тел.

В теории гравитации Ньютона М. выступает в другой форме — как источник поля тяготения. Каждое тело создаёт поле тяготения, пропорциональное М. тела (и испытывает воздействие поля тяготения, создаваемого другими телами, сила которого также пропорциональна М. тел). Это поле вызывает притяжение любого другого тела к данному телу с силой, определяемой Ньютона законом тяготения (См. Ньютона закон тяготения ):

, (3)

В принципе ниоткуда не следует, что М., создающая поле тяготения, определяет и инерцию того же тела. Однако опыт показал, что инертная М. и гравитационная М. пропорциональны друг другу (а при обычном выборе единиц измерения численно равны). Этот фундаментальный закон природы называется принципом эквивалентности. Его открытие связано с именем Г. Галилея (См. Галилей ), установившего, что все тела на Земле падают с одинаковым ускорением. А. Эйнштейн положил этот принцип (им впервые сформулированный) в основу общей теории относительности (см. Тяготение ). Экспериментально принцип эквивалентности установлен с очень большой точностью. Впервые (1890—1906) прецизионная проверка равенства инертной и гравитационной М. была произведена Л. Этвеш ем, который нашёл, что М. совпадают с ошибкой ~ 10^-8. В 1959—64 американские физики Р. Дикке, Р. Кротков и П. Ролл уменьшили ошибку до 10^-11, а в 1971 советские физики В. Б. Брагинский и В. И. Панов — до 10^-12.

Принцип эквивалентности позволяет наиболее естественно определять М. тела Взвешивание м.

Первоначально М. рассматривалась (например, Ньютоном) как мера количества вещества. Такое определение имеет ясный смысл только для сравнения однородных тел, построенных из одного материала. Оно подчёркивает аддитивность М. — М. тела равна сумме М. его частей. М. однородного тела пропорциональна его объёму, поэтому можно ввести понятие плотности (См. Плотность ) — М. единицы объёма тела.

В классической физике считалось, что М. тела не изменяется ни в каких процессах. Этому соответствовал закон сохранения М. (вещества), открытый М. В. Ломоносов ым и А. Л. Лавуазье . В частности, этот закон утверждал, что в любой химической реакции сумма М. исходных компонентов равна сумме М. конечных компонентов.

Понятие М. приобрело более глубокий смысл в механике спец. теории относительности А. Эйнштейна (см. Относительности теория ), рассматривающей движение тел (или частиц) с очень большими скоростями — сравнимыми со скоростью света с — 3․10¹⁰ см/сек . В новой механике — она называется релятивистской механикой — связь между импульсом и скоростью частицы даётся соотношением:

(5)

При малых скоростях ( v 0называют массой покоя, а М. движущейся частицы m определяют как зависящий от скорости коэфф. пропорциональности между р и v :

(6)

Имея в виду, в частности, эту формулу, говорят, что М. частицы (тела) растет с увеличением её скорости. Такое релятивистское возрастание М. частицы по мере повышения её скорости необходимо учитывать при конструировании ускорителей заряженных частиц (См. Ускорители заряженных частиц ) высоких энергий. М. покоя m ₀(М. в системе отсчёта, связанной с частицей) является важнейшей внутренней характеристикой частицы. Все элементарные частицы обладают строго определёнными значениями m ₀, присущими данному сорту частиц.

Следует отметить, что в релятивистской механике определение М. из уравнения движения (2) не эквивалентно определению М. как коэффициент пропорциональности между импульсом и скоростью частицы, так как ускорение перестаёт быть параллельным вызвавшей его силе и М. получается зависящей от направления скорости частицы.

Согласно теории относительности, М. частицы m связана с её энергией Е соотношением:

(7)

М. покоя определяет внутреннюю энергию частицы — так называемую энергию покоя Е ₀= m ₀ c² . Таким образом, с М. всегда связана энергия (и наоборот). Поэтому не существует по отдельности (как в классической физике) закона сохранения М. и закона сохранения энергии — они слиты в единый закон сохранения полной (то есть включающей энергию покоя частиц) энергии. Приближённое разделение на закон сохранения энергии и закон сохранения М. возможно лишь в классической физике, когда скорости частиц малы ( v

В релятивистской механике М. не является аддитивной характеристикой тела. Когда две частицы соединяются, образуя одно составное устойчивое состояние, то при этом выделяется избыток энергии (равный энергии связи (См. Энергия связи )) Δ Е , который соответствует М. Δ m = Δ Е/с² . Поэтому М. составной частицы меньше суммы М. образующих его частиц на величину Δ Е/с² (так называемый Дефект масс ). Этот эффект проявляется особенно сильно в ядерных реакциях (См. Ядерные реакции ). Например, М. дейтрона (d) меньше суммы М. протона (p) и нейтрона (n); дефект М. Δ m связан с энергией Е _γгамма-кванта (γ), рождающегося при образовании дейтрона: p + n → d + γ, = Δ · . Дефект М., возникающий при образовании составной частицы, отражает органическую связь М. и энергии.

Единицей М. в СГС системе единиц служит Грамм , а в Международной системе единиц (См. Международная система единиц ) СИ — Килограмм . М. атомов и молекул обычно измеряется в атомных единицах массы (См. Атомные единицы массы ). М. элементарных частиц принято выражать либо в единицах М. электрона m _e, либо в энергетических единицах, указывая энергию покоя соответствующей частицы. Так, М. электрона составляет 0,511 Мэв , М. протона — 1836,1 m _e, или 938,2 и т. д.

Природа М. — одна из важнейших нерешенных задач современной физики. Принято считать, что М. элементарной частицы определяется полями, которые с ней связаны (электромагнитным, ядерным и другими). Однако количественная теория М. ещё не создана. Не существует также теории, объясняющей, почему М. элементарных частиц образуют дискретный спектр значений, и тем более позволяющей определить этот спектр.

В астрофизике М. тела, создающего гравитационное поле, определяет так называемый Гравитационный радиус тела R _гр= 2GM/c² . Вследствие гравитационного притяжения никакое излучение, в том числе световое, не может выйти наружу, за поверхность тела с радиусом R ≤ R _гр. Звёзды таких размеров будут невидимы; поэтому их назвали «чёрными дырами (См. )». Такие небесные тела должны играть важную роль во Вселенной.

Лит.: Джеммер М., Понятие массы в классической и современной физике, перевод с английского, М., 1967; Хайкин С. Э., физические основы механики, М., 1963; Элементарный учебник физики, под редакцией Г. С. Ландсберга, 7 изд., т. 1, М., 1971.

Я. А. Смородинский.

IV

Ма́сса (Massa)

город в Центральной Италии, в Тоскане, близ берега Лигурийского моря (аванпорт Марина-ди-Масса). Административный центр провинции Масса-э-Каррара. 62,8 тысячи жителей (1971). Производство изделий из каррарского мрамора, добываемого в Апуанских Альпах. Машиностроение (энергетическое и химическое оборудование), небольшая металлургическая и химическая промышленность.

Вес тела примеры. Вес тела

В обычной жизни вес считается синонимом массы. Но в физике вес и масса – разные вещи.

Вес тела (обозначается Р ) – сила, с которой тело действует на опору или подвес из-за притяжения к Земле.

У космонавтов в состоянии невесомости есть масса, но нет веса. Каждый человек достигаетневесомости, если отрывает обе ноги от земли при беге.

Если тело покоится или двигается равномерно, его вес вычисляется по формуле:

Коэффициент g различается в разных точках Земли и на других планетах. В Минске человекбудет весить меньше, чем в Москве. Коэффициент g для различных мест:

При покое и равномерном движении модули (числовое значение) веса тела и силы тяжестиравны. Но, если тело ускоряется, замедляется или двигается по кривой, они отличаются.Когда лифт разгоняется и двигается вниз, тело меньше давит на пол и вес уменьшается, а когдадвигается вверх, давление на опору и вес увеличиваются. Это чувствуется даже по ощущениям:при подъёме тело как бы вжимается в пол. Изменение веса можно подтвердить иэкспериментально, если проехаться в лифте, стоя на весах.

Изменение веса, вызванное изменением скорости, – это перегрузка.

На карусели или в набирающей скорость машине перегрузка вдавливает тело в сидение.Громадные перегрузки испытывают пилоты: при совершении фигур высшего пилотажа их вес (азначит, вес всех органов, костей, крови) растёт в 10–20 раз. Сила мышц при этом неувеличивается. Сердечная мышца обычного человека не может проталкивать такую тяжёлуюкровь к голове, поэтому при высоких перегрузках он теряет сознание. Поэтому пилотовтренируют выдерживать 10-кратный вес на центрифуге – это, по сути, быстро вращающаясякарусель.

Вопросы:

1. Чем отличаются вес тела и масса тела?2. Может ли вес тела быть равным нулю?3. Как найти вес покоящегося тела?4. Что такое перегрузка?5. Будет ли вес тела на Луне отличаться от веса этого же тела на Земле?6. Насколько будет отличаться ваш вес в столице Республики Беларусь от веса в столице США?

Вес формула. Понятие веса тела

Понятие «вес» как таковое в физике не считается необходимым. Так, больше говорится о массе или о силе тела. Более содержательной величиной считается сила воздействия на опору, знание которой может помочь, например, при оценке способности конструкции удержать исследуемое тело в заданных условиях.

Вес возможно измерить с помощью пружинных весов, служащих также для косвенного измерения массы при их соответствующем градуировании. В то же время, рычажные весы в этом не нуждаются, поскольку в такой ситуации сравнению подлежат массы, на которые воздействует равное ускорение свободного падения либо сумма ускорений в неинерциальных системах отсчета.

При взвешивании за счет технических пружинных весов, вариации ускорения свободного падения обычно не учитываются, поскольку из влияние зачастую оказывается меньше того, что требуется на практике в отношении точности взвешивания. В некоторой степени, на результатах измерений может отражаться сила Архимеда, при условии взвешивания на рычажных весах тел различной плотности и их сравнительных показателей.

Вес и масса в физике представляют различные понятия. Так, вес считается векторной величиной, с которой тело будет непосредственно воздействовать на горизонтальную опору либо вертикальный подвес. Масса в то же время представляет скалярную величину, меру инертности тела (инертную массу) или заряд гравитационного поля (гравитационную массу). У таких величин будут отличаться и единицы измерения (в СИ масса обозначена в килограммах, а вес— в ньютонах).

Возможны также ситуации с нулевым весом и также ненулевой массой (когда речь идет об одном и том же теле, к примеру, при невесомости вес каждого тела будет равным нулевому значению, а вот масса у всех окажется разной).

Вес тела рисунок. Сила тяжести. Вес, невесомость, перегрузки

Урок 19. Физика 10 класс

На этом уроке мы познакомимся с понятием веса в физике и убедимся, что он может зависеть от того, с каким ускорением двигается тело. С этим связаны понятия невесомости и перегрузки.

Вы уже знакомы с понятием силы тяжести — это сила, с которой Земля притягивает тело, находящееся на её поверхности (или вблизи этой поверхности). Именно под действием силы тяжести, тела могут находиться в свободном падении. Находясь в свободном падении можно ясно ощутить состояние невесомости, то есть, отсутствие веса . Рассмотрим эти явления более подробно.

Еще в седьмом классе вы познакомились с весом тела. Вес тела — это сила, с которой тело действует на горизонтальную опору или растягивает подвес. Надо сказать, что вес — это частный случай силы упругости . Рассмотрим простой пример. В помещении вы видите сидящего человека, горшки с растениями, часы, висящие на стене и так далее. На все эти тела, несомненно, действует сила тяжести.

Несмотря на это, все тела находятся в состоянии покоя. Дело в том, что опора, по третьему закону Ньютона, действует, например, на горшок, с той же силой, что и горшок давит на неё. Эта сила называется реакцией опоры. Итак, мы выяснили что, исходя из третьего закона Ньютона , реакция опоры равна по модулю весу тела. Поскольку тело покоится, равнодействующая сила равна нулю. Следовательно, реакция опоры должна уравновешивать силу тяжести (в противном случае, тело бы падало по направлению к центру Земли).

Таким образом, если тело покоится на горизонтальной поверхности, или двигается равномерно и прямолинейно, то вес тела равен силе тяжести .

А теперь, давайте рассмотрим, что произойдет, если опора будет двигаться с ускорением. Классический пример подобной ситуации — это движение лифта. При начальном движении лифта вверх, ускорение, конечно, направлено вверх.

Применим второй закон Ньютона:

Из этого уравнения, мы видим, что вес тела увеличивается при ускоренном движении опоры вверх. Это явление называется перегрузкой . Действительно, при рывке лифта вверх, мы чувствуем некое давление.

Нетрудно догадаться, что при ускоренном движении вниз, происходит противоположное явление: вес тела уменьшается.

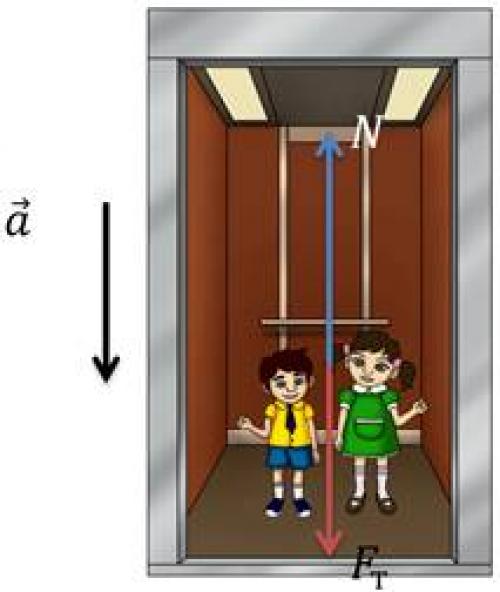
В этом можно убедиться, если вновь применить второй закон Ньютона:

Как видно, из уравнения, при движении вниз с ускорением свободного падения, вес тела обратится в ноль:

Это явление называется невесомостью . И правда, при рывке лифта вниз, мы ощущаем некую легкость.

Так, космонавты, находящиеся на космической станции, испытывают состояние невесомости. Они, фактически находятся в свободном падении, но падают, как бы, вокруг Земли. Дело, конечно, в их орбитальной скорости, достаточной для того, чтобы находиться на околоземной орбите.

Приведем пару примеров. Допустим, вы поставите стакан с водой на поднос. Очевидно, что стакан будет действовать на поднос с силой: F _т= mg . Но, как вы знаете, если вы отпустите поднос, то и стакан, и поднос будут находиться в свободном падении.

При этом, стакан не будет оказывать никакого воздействия на поднос, то есть не будет обладать весом. Точно также, мотоциклист, едущий с постоянной скоростью, будет действовать на сиденье мотоцикла силой тяжести. Но после прыжка на трамплине, и мотоциклист, и мотоцикл будут находиться в свободном падении.

Таким образом, вес мотоциклиста будет равен нулю, до тех пор, пока он не приземлится.

Примером перегрузки может быть выход пилота из пике.

В нижней точке, его центростремительное ускорение будет направлено вверх, что приведет увеличению веса пилота. Пилоты истребителей испытывают перегрузки до 30 g . Перегрузки часто измеряются в единицах измерения g . То есть, например, перегрузка 5 g означает, что вес пилота увеличился в 6 раз (в состоянии покоя наша перегрузка равна g ). Иногда перегрузку обозначают буквой n , и она является безразмерной величиной, равной отношению ускорения движения к ускорению свободного падения.

Таким образом, вес тела при перегрузках можно вычислить по формуле:.

Для примера вычислим перегрузку, которую испытывает пилот в нижней точке пике в вертикальной плоскости, если радиус кривизны траектории полёта равен 400 м, а скорость самолёта равна 1080 км/ч.