Интересные факты геометрия. Интересные факты о геометрии

Интересные факты геометрия. Интересные факты о геометрии

1. Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
2. Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
3. С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
4. Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
5. Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
6. Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
7. В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
8. Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
9. Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
10. Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
11. Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
12. Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
13. Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
14. При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
15. Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.

История развития геометрии Интересные факты. «Школьная газета » Интересные факты о геометрии»

Интересные факты о геометрии.Слово «трапеция» произошло от древнегреческого слова «трапезион»(обозначает столик). также от данного слова произошли уже немногоподзабытые в обиходе слова, такие как «трапеза» и прочие родственныеему слова.Математика для древних греков была, прежде всего, геометрией.Поэтому над двери Академии, в стенах которой Платон учил своих учеников, висела надпись: «Пусть сюда не входит тот, кто не знает геометрии».Греческое слово «конос», обозначающее сосновую шишку, является словарной основой для такого термина как «конус», а известный в геометрии термин «линия» возник уже от латинского слова «линум» (что в переводе на русский язык означает «льняная нить»).Пирог разрезается всего тремя касаниями ножа на восемь равных долей. Причем, существует только два способа это сделать. Под треугольником Рёло понимают геометрическую фигуру, образованную пересечением 3 кругов одинакового радиуса D с центрами, находящимися в вершинах равностороннего треугольника, такой же по длине стороны. на основе треугольника Рёло было придумано сверло, позволяющее просверливатьпочти квадратные отверстия. В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180. В геометрии Римана сумма углов треугольника всегда больше 180.Если число 111 111 111 помножить на себя самого, то получится интересное число 12 345 678 987 654 321 (все числа сначала возрастают, а потом убывают по порядку).Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.Еще факты Знаете ли вы? Что Шарль Перро, автор «Красной Шапочки», написал сказку «Любовь циркуля и линейки»?   Что Наполеон Бонапарт писал математические труды и один геометрический факт называется «Задача Наполеона»?   Что Пифагор был победителем из кулачного боя на 58-х Олимпийских играх, проходивших в 548 году до н. э., а затем побеждал еще на нескольких Олимпиадах? Выполнил Меркулов Лев,Педагог Меркулова О.Р.

Интересные факты о конусе. Конусы

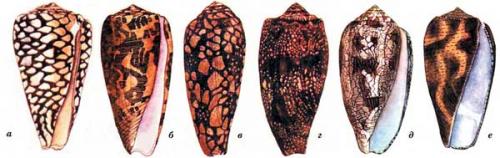
Брюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.

K наиболее распространенным и брюхоногих моллюсков рода конус относятся:

• , живущие в зоне от Полинезии до Индийского океана;
• , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
• обитающие в регионе от Красного моря до Полинезии;
• - житель берегов Австралии и восточного побережья Африки.

Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.

Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун - зубы радулы.

Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.

Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.

Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.

Интересные факты о углах. 10 интересных фактов о математике, которые удивляют

Человек может и не быть математиком. 

Более того, он может даже не знать эту науку на минимальном уровне, но тяжело отрицать – математику человек видит практически везде. 

Цифры, фигуры и математические законы преследуют человека повсюду, поэтому нелишним будет узнать кое-что об этой науке.

1. Абрахам де Муавр (математик из Англии) в своей глубокой старости вдруг понял, что его сон увеличивается на 15 минут в каждый последующий день. После этого он составил прогрессию и определил тот день, когда сон займет весь день. Случилось это 27 ноября в 1754 году, и это был день его смерти.

2. Религиозные и верующие евреи стараются всеми силами избегать любых знаков, которые связаны с крестом или символику Христа. К примеру, вместо плюса в школах используют перевернутую «Т».

3. Подлинность денежной купюры евро всегда можно узнать по ее серийному номеру – это буква и 11 цифр. Необходимо поменять букву на то число, которое является порядковым номером этой буквы в алфавите. После этого необходимо сложить все числа и складывать результаты до тех пор, пока не будет одна цифра. И если в итоге получится 8, это говорит о подлинности купюры. Другой способ – сложение всех цифр, без буквы. Итоговый результат, состоящий их буквы и цифры, должен подходить под ту страну, на территории которой появилась купюра. К примеру, Германия – это Х2.

4. Есть версия, что Альфред Нобель отказался включать математику в длинный список наук для своей премии по личным причинам – жена Альфреда спала с математиком. Но в действительности Нобель был холостым. Нет достоверных доказательств того, почему математику не включили, однако есть предположения. К примеру, уже тогда существовала своя премия, но созданная шведским королем. Другая версия – математика является чисто теоретическим предметом, поэтому математики не способны сделать ничего действительно важного для людей и человечества в целом.

5. Есть такая фигура, как треугольник Рело. Она образовывается через пересечение трех идентичных по радиусу кругов, причем центры этих кругов расположены в вершинах треугольника с равными сторонами. Сверло, созданное на основе этого треугольника, дает возможность сверлить только квадратные отверстия. При этом стоит помнить, что сверление таких отверстий с использованием треугольника Рело может иметь погрешность в 2 процента.

6. В русской литература и математике 0 не относится к спискам натуральных чисел, однако на западе 0 является одним из представителей множества таких чисел.

7. Джордж Данциг, математик из Америки, будучи всего лишь университетским аспирантом, один раз опоздал на занятие и, увидев несколько уравнений и подумал о том, что эти уравнения являются общими домашними задачами, которые необходимо выполнить. Это задание показалось ему намного сложнее того, что давали обычно, но он их выполнил и принес результаты преподавателю. И только после этого он узнал, что смог решить 2 нерешаемых уравнения статистики. Причем это были те задачи, которые не могли решить ученые в течение нескольких лет.

8. Если сложить все числа в рулетке, получится 666.

9. Небезызвестная Софья Ковалевская познакомилась с этой наукой о числах в далеком детстве – в ее комнате не было обоев, были лишь лекции ученого Остроградского об исчислениях.

10. В Индиане (штат США) в 1897-ом году выпустили билль, согласно которому число Пи будет равно 3,2. Однако билль не превратился в закон благодаря тому, что в этот процесс вовремя вмешался университетский профессор.

Интересные факты о стереометрии. Изображение пространственных объектов

В планиметрии мы изучали свойства плоских фигур. Хотя в природе их не найдешь – любой объект объёмный. Почему же мы так много времени уделили плоским фигурам, которых не существует в окружающем мире?

Есть природа, а есть модели природных объектов, которые у нас получается исследовать – отрезки, углы, фигуры. Они, в свою очередь, являются элементами объёмных тел. Изучив подробно свойства плоских фигур, теперь мы сможем применять полученные знания для исследования тел в пространстве.

Кирпич имеет форму параллелепипеда, а его грани – форму прямоугольника. Бревно имеет форму цилиндра, а спил (сечение) – форму круга, если спил сделан перпендикулярно оси бревна, и эллипса, если под углом.

То есть переход от планиметрии к стереометрии – это расширение математической модели, а не замена одной на другую.

В планиметрии с изображением фигур было все просто: лист бумаги, по сути, представлял плоскость, и изобразить на нём плоскую фигуру (например, квадрат со стороной а) не составляло труда.

В стереометрии мы будем объёмные фигуры изображать на плоскости, что потребует от нас определенных навыков.

Особенности нашего зрения

Мы привыкли доверять своим глазам и не задаемся вопросом, почему один и тот же объект вблизи выглядит крупнее, чем вдали? Или почему разные по величине предметы порой кажутся одного размера? Механизмы зрения довольно сложны, однако некоторые его особенности можно объяснить на основе геометрических представлений.

Всякий предмет имеет линейные размеры: длину, ширину и высоту. Но как только он попадает в наше поле зрения, то приобретает еще один размер – угловой. Давайте разберемся, что это означает. Когда мы смотрим на предмет, то через каждую его точку можно провести от глаза луч, называемый лучом зрения. Понятно, что их будет бесконечно много. Любые два луча зрения образуют угол зрения (см. рис. 1).

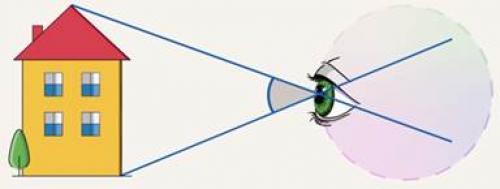
Рис. 1. Угол зрения

Тот угол зрения, под которым предмет виден целиком, и принято называть угловым размером предмета. Как и всякий плоский угол, он измеряется в градусах, минутах, секундах или в радианах.

Угловой размер предмета – величина не постоянная и зависит от расстояния предмета от глаза: чем предмет дальше, тем меньше угол зрения, под которым он виден.

Чтобы понять причину этого явления, вспомним, что на сетчатке глаза изображение предмета получается обратным и уменьшенным. При удалении предмета его изображение на сетчатке становится меньше, поэтому он и кажется нам уменьшающимся (см. рис. 2). При сокращении расстояния изображение, напротив, увеличивается, и предмет кажется увеличивающимся (см. рис. 3).

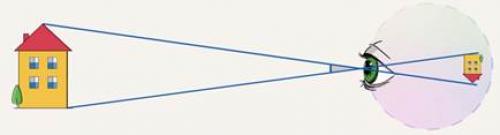
Рис. 2. Предмет кажется уменьшающимся при его удалении

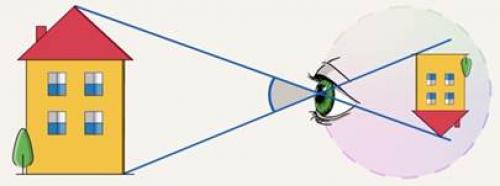
Рис. 3. Предмет кажется увеличивающимся при его приближении

Теперь легко объяснить, почему две «убегающие» вдаль параллельные линии (железнодорожные рельсы, края прямолинейного шоссе) кажутся «сходящимися» в одной точке (см. рис. 4). Такое же впечатление создают ряды телеграфных столбов или деревьев вдоль дороги. Это лишь иллюзия, которая возникает из-за видимого уменьшения расстояния между прямыми по мере их удаления.

Рис. 4. Железнодорожные рельсы кажутся «сходящимися» в одной точке

Часто приходится сталкиваться и с другой ситуацией. Если рассматривать предметы одинаковой формы, но разных линейных размеров под одним и тем же углом зрения, то кажется, что их размеры равны. Поэтому мы можем закрыть монеткой Луну или Солнце.

А при полном солнечном затмении лунный диск в точности заслоняет солнечный (см. рис. 5). В этот момент наблюдатель с Земли видит оба небесных тела под одним углом зрения.

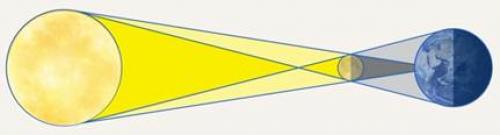
Рис. 5. При полном солнечном затмении лунный диск в точности заслоняет солнечный

Увидеть такое уникальное явление было бы невозможно, если бы линейные размеры Солнца и Луны, а также расстояния от них до Земли не состояли в определенной математической зависимости: диаметры Солнца и Луны (и) и расстояния от этих тел до Земли (и) связаны пропорцией:

Исходя из указанных особенностей нашего зрения, важно научиться правильно изображать объекты, чтобы избежать оптического обмана и искажения восприятия.

Работая с такими фигурами, необходимо научиться изображать их на бумаге. Для этого нужно следовать двум соображениям:

1. При изображении дли́ны отрезков и величи́ны углов могут меняться, т.е. длинный отрезок вполне может быть изображен коротким, а прямой угол острым или тупым;
2. Параллельность отрезков сохраняется всегда. Длины параллельных отрезков меняются в одинаковой степени, т.е. параллельные равные отрезки всегда будут изображены тоже как параллельные и равные.

Пока мы будем использовать эти утверждения без доказательства, так как у нас не хватает теоретической базы. Но скоро мы сможем это сделать. А пока потренируемся изображать различные тела.